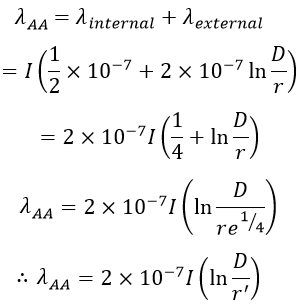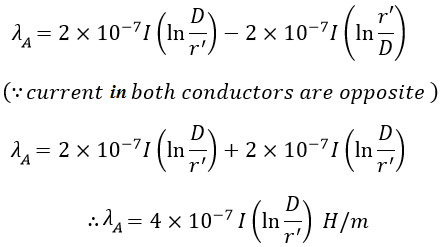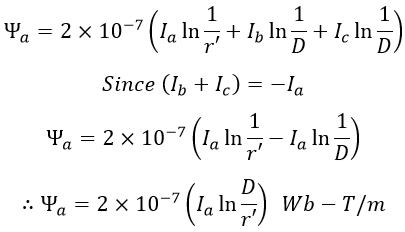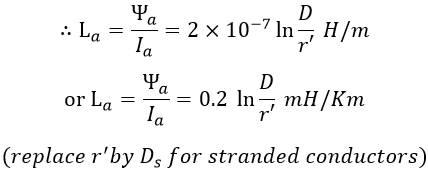When the conductors of the transmission line carry alternating current, an alternating magnetic flux will be set up by the conductors. Due to the alternating nature of current, the flux linkages with the conductor change and hence causes inductance (induced emf) to be present in the conductor. The inductance of a conductor is given by the ratio of total magnetic flux linkages to the current flowing through it.
The total magnetic flux linkage is flux linkage to a conductor due to its own current and due to current in the neighboring conductors. Let us see the expressions for the inductance of a conductor in single-phase and three-phase transmission lines.
Inductance of Singe-Phase Transmission Line :
Consider a single-phase overhead transmission line consisting of conductors A and B of radius r, spaced at a distance D apart as shown in the figure below. Let the conductors carry equal currents but as one conductor is 'go' and another is 'return', the sum of the currents is zero.
The total flux linkage of any conductor (say A) is due to its own current, called the internal flux linkage, and the current in the adjacent conductor, called the external flux linkage.
Inductance of a Conductor due to Internal Flux :
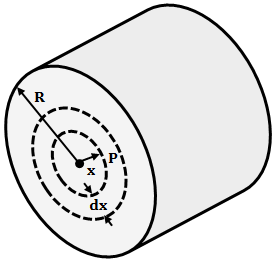
Concentrating on conductor A of the above figure. Consider a point P at a radial distance of x m from the center of the conductor A. Such that x < R as shown below.
According to Ampere's Circuital Law, the field strength H at a radial distance x from the center of the conductor is given by,
If I, is the current flowing in the conductor, then the current enclosed within the region of the radius is given by,I' = I(x/R)2Therefore, the field strength is given as,
We know that magnetic flux density B is given by,
Now, the total flux crossing the region of thickness dx and axial length one meter is given by,
Therefore, the flux linking with the region of radius x is given by,
The total flux linkage with the conductor from its center to the surface is given by,
The inductance of conductor A due to internal flux linkage λint is,
Thus, the inductance per unit length of a conductor due to internal flux linkage is constant and is independent of the size of the conductor.
Inductance of a Conductor due to External Flux :
Consider the two points Q and R lying at a distance of R1, R2 respectively from the center of the conductor A as shown in the figure below.
According to Ampere's Circuital Law, the field strength at a point P distance x from the center of the conductor A such that x > r is given by,
We know that, magnetic flux density is given by,B = µoH = µoI/2πx Wb/m2Now, the total flux crossing the region of thickness dx and axial length one meter is given by,
This flux links all the current in the conductor only once. Because all the flux is external to the conductor.∴ dλ = µoI/2Ï€x dxThe total external flux linkages between points Q and R is given by,
The inductance of conductor contributed by the flux including points Q and R is,
Let the external point be at a distance D from the center of the conductor. The inductance of conductor A due to external flux linkage can be found by substituting R1 = r and R2 = (D - r).
Inductance of a Single-Phase Transmission Line :
We know that the flux linkage of a conductor is the sum of the internal and external flux linkages. Therefore the flux linkage of conductor A due to its own current is,
Where, r' = re-1/4 = 0.7788 x r = Geometric Mean Radius. Similarly, the flux linkage of conductor A due to current in another conductor is,
The flux linkage of conductor A due to current in both the conductors is,
The inductance L of a single-phase circuit (which is loop inductance) is given by,
Inductance of Three-Phase Transmission Line with Symmetrical Spacing :
Consider a 3-phase overhead transmission line with phase conductors a,b,c and are symmetrically spaced i.e., conductors are placed equidistant from each other as shown below. Let D be the distance between the conductors and r be the radius of each conductor.
Let Ia, Ib, and Ic be the currents of conductors a, b, and c. If the currents are assumed to be balanced, then,
The flux linkage of conductor 'a' due to currents Ia, Ib and Ic is given by,
Therefore, the inductance of conductor 'a' is given as,
Since the conductors are symmetrically spaced, the inductance per conductor is same for all the conductors. Hence, the inductance of conductors b and c is equal to the inductance of conductor a when they are symmetrically spaced.
