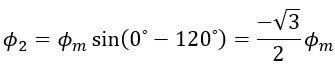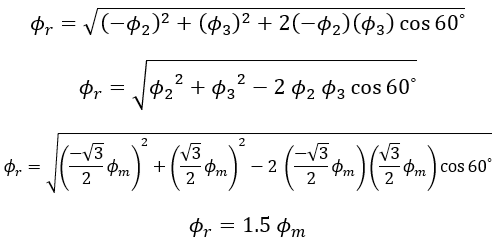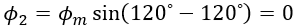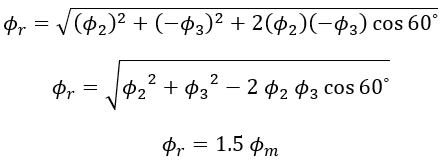When a magnet or magnetic pole ( coil or winding ) is rotated, the magnetic field or flux of constant amplitude produced by the magnet or poles will be a rotating magnetic field. But in this case, an external physical force is needed to rotate magnet or coils.
In practice, without any external force, a rotating magnetic field can be produced with the help of a polyphase ac supply. When the three-phase uniformly distributed winding suitably wound on the stator is supplied with a 3-phase ac supply, a rotating magnetic field of constant magnitude rotating at synchronous speed is produced. Let us see how it is possible.
Consider 3-phase, 2 pole stator having three similar windings aa', bb', and cc' displaced in space by 120°, supplied with 3-phase ac supply as shown below.
Due to the current flowing in each phase displaced from each other by 120° produces an alternating flux which is assumed to be sinusoidal in nature. The fluxes produced by each phase Φ1, Φ2, and Φ3 are also displaced by 120° from each other. The instantaneous values of fluxes with respect to time is given by,
Where Φm = maximum value of the flux due to any phase. The waveforms of these fluxes and their phase representation are shown below.
The three fluxes together give rise to the effect of rotating flux called Rotating Magnetic Field. At any instant, the resultant flux, Φr is the phasor sum of the fluxes of the three phases (Φ1, Φ2, and Φ3) at that instant. Let us see four different instants 0 (0⁰), 1 (60⁰), 2 (120⁰), and 3(180⁰) as shown in the above waveform.
i. When θ = 0⁰ (At point 0) :
At point 0 on the waveform i.e, at 0⁰, the value of Φ1 is,
The value of Φ2 is,
The value of Φ3 is,
Since Φ1 = 0, the resultant of Φ2 and Φ3 can be found out by reversing Φ2 and adding it with Φ3 as shown below.
From the figure Resultant flux Φr,
So at 0⁰, the magnitude of resultant flux is 1.5 times the maximum value of individual flux.
ii. When θ = 60⁰ (At point 1) :
At point 1 on the waveform i.e, at 60⁰, the value of Φ1 is,
The value of Φ2 is,
The value of Φ3 is,
Since Φ3 = 0, the resultant of Φ1 and Φ2 can be found out by reversing Φ2 and adding it with Φ1 as shown below.
From the figure Resultant flux Φr,
Therefore at 60⁰, the magnitude of resultant flux Φr = 1.5 Φm. Here we can notice that the magnitude of Φr is the same as that of the previous, also the phasor has rotated clockwise through an angle of 60⁰.
iii. When θ = 120⁰ (At point 2) :
At point 2 on the waveform i.e, at 120⁰, the value of Φ1 is,
The value of Φ2 is,
The value of Φ3 is,
Since Φ2 = 0, the resultant of Φ1 and Φ3 can be found out by reversing Φ3 and adding it with Φ1 as shown below.
From the figure Resultant flux Φr,
Therefore at 120⁰, the magnitude of resultant flux Φr = 1.5 Φm. Here also, the magnitude of Φr is the same as that at 0⁰ and 60⁰, but the phasor has further rotated clockwise through an angle of 60⁰ or 120⁰ from the start.
iv. When θ = 180⁰ (At point 3) :
At point 3 on the waveform i.e, at 180⁰, the value of Φ1 is,
The value of Φ2 is,
The value of Φ3 is,
Since Φ1 = 0, the resultant of Φ2 and Φ3 can be found out by reversing Φ3 and adding it with Φ2 as shown below.
From the figure Resultant flux Φr,
