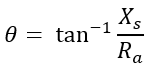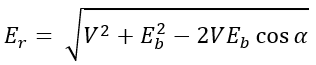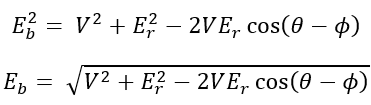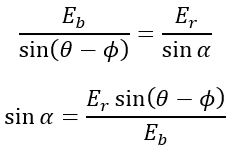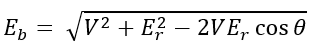Phasor Diagram & Back EMF of Synchronous Motor

In this article let us draw the phasor diagram of synchronous motor and also derive the expression for back emf E_b and load angle α for various factors.

Analysis of Phasor Diagram Under Normal Conditions :

Let,

• V = Supply voltage per phase
• I_a = Armature current per phase
• Φ = p.f. angle or angle between V and I_a
• cos Φ = p.f. at which motor is working
• α = Load angle or Torque angle corresponding to the load on the motor

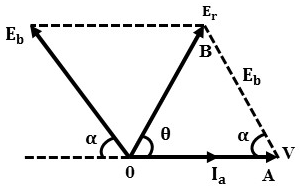
The phasor diagram with all the above details at normal excitation is shown below.

When the value of back emf is equal to applied voltage E_b = V then the synchronous motor is said to be at normal excitation. The angle θ is called an internal machine angle or impedance angle. It is constant for a motor.

The significance of θ is that it tells us that I_a lags behind E_r by an angle θ. Practically armature resistance R_a is very small compared to reactance X_s and hence θ tends to 90°. It is expressed as,

From the phasor diagram, armature current is given by I_a = E_r / Z_s and, synchronous impedance Z_s = R_a + jX_s. The vector difference of E_b and V gives the resultant emf E_r which represents I_a Z_s. The resultant emf E_r is expressed as,

The nature of the power factor is lagging if I_a lags V by angle Φ while it is leading if I_a leads V by angle Φ. Let us see the phasor diagram and expression for back emf and load angle at different power factor loads.

Phasor Diagram at Lagging PF :

When field excitation is made in such a way that back emf is less than the applied voltage (E_b < V) then the motor is said to be 'Under-Excited'. Here the torque angle α is small and I_a lags behind V with poor power factor angle Φ. The phasor diagram is shown below.

Applying cosine rule to triangle OAB,

Applying sine rule to triangle OAB,

Hence load angle α can be calculated once E_b is known.

Phasor Diagram at Leading PF :

When excitation is increased in such a way that E_b > V, the motor is said to be 'Over-excited'. Here the current I_a is comparatively larger and leads the voltage V by an angle Φ as shown below.

Applying cosine rule to triangle OAB,

Applying sine rule to triangle OAB,

Hence load angle α can be calculated once E_b is known.

Phasor Diagram at Unity PF :

The change in excitation for which the armature current will be in phase with voltage so that power factor becomes unity, this occurs when E ≅ V. Therefore Φ = 0 and cos Φ = 1.

Applying cosine rule to triangle OAB,

Applying sine rule to triangle OAB,