Double Revolving Field Theory

When a single-phase ac supply is given to the single-phase stator winding, a sinusoidally pulsating magnetic field varying with time is produced. As the produced magnetic very two times in a cycle, therefore, no torque will be produced in the rotor and hence the rotor doesn't rotate. Therefore, single-phase induction motors are not self-starting motors.

However, when an initial rotation is given to the rotor, it starts rotating in that direction which can be explained by the double-revolving field theory.

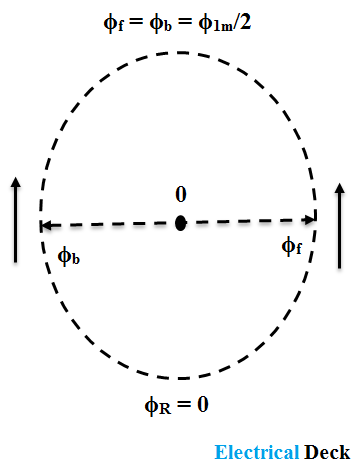
The magnetic field produced by the stator winding when an alternating supply is given is equal to the sum of the two revolving fields rotating at synchronous speed in the opposite direction of equal magnitude. The magnitude of each revolving field is equal to one-half of the maximum value of the alternating field, i.e., Φ_1m/2, where Φ_1m is the maximum value of an alternating field.

Let us consider the two revolving fields as Φ_f (rotating in an anti-clockwise direction) and Φ_b (rotating in a clockwise direction). The resultant Φ_R of these two fields gives the value of the magnetic field produced by the alternating supply (i.e., alternating field).

Consider the Different Instances as Shown Below :

The two fields Φ_f and Φ_b are shown opposite to each other at the start, and the resultant magnetic field Φ_R = 0.

After 90°, the two fields are rotated in such a way that both of them are now pointing in the same direction. The resultant magnetic field,

This instant gives maximum the magnitude of the original alternating field. So the continuous rotation of these two fields (components) gives the original stator magnetic field. This is purely alternating in nature.

Now each separate component is rotated and hence gets cut by the rotor conductors. Due to cutting of flux emf gets induced in rotor conductors which circulate in the rotor current. The rotor current produces rotor flux.

The rotor flux interacts with one component Φ_f produces a torque in an anti-clockwise direction and the rotor flux interacts with the second component Φ_b produces a torque in a clockwise direction.

If anticlockwise torque is assumed positive, then the clockwise torque produced by another is negative. The resultant of the two torques at the start is zero. Torque-speed characteristics are shown below.

Following are Important Points About the Resultant Magnetic Field :

1. At the start, the two torques are equal in magnitude but opposite in direction. These two torques try to rotate the rotor in different directions. Hence net torque experienced by the rotor is zero. Therefore it is said that single-phase induction motors are not self-starting.
2. When initial rotation is given to the rotor in any direction, the overall torque increases in that direction and the motor starts giving performance similar to the 3-phase induction motor.